Το θεώρημα προβλέπει ότι η μελλοντική συναλλαγματική ισοτιμία θεωρητικά θα προσαρμοστεί έτσι, ώστε οι επενδυτές να απολαμβάνουν την ίδια τελική απόδοση επένδυσης ανεξάρτητα της χώρας επένδυσης.
Με άλλα λόγια, η διαφορά μεταξύ των επιτοκίων δύο χωρών ισούται με την διαφορά μεταξύ της μελλοντικής (forward) και της παρούσας (spot) συναλλαγματικής ισοτιμίας.
Αν μια χώρα προσφέρει υψηλότερα επιτόκια (risk free rates) σε ένα νόμισμα από αυτό μιας άλλης, το νόμισμα της χώρας που προσφέρει το υψηλότερο επιτόκιο θα συναλλάσσεται σε υψηλότερη μελλοντική τιμή απ’ ότι η τρέχουσα. Με αυτό το τρόπο στην ουσία εξασφαλίζεται ότι δεν υπάρχει περιθώριο αθέμιτης εξισορροπητικής κερδοσκοπίας (arbitrage) στην αγορά συναλλάγματος. Ένας επενδυτής δεν μπορεί δηλαδή να αγοράζει φθηνά ένα νόμισμα και να επενδύει στην χώρα με την υψηλότερη απόδοση χωρίς κόστος.
Η σχέση που προκύπτει από το θεώρημα είναι η ακόλουθη:
[Προθεσμιακή συναλλαγματική ισοτιμία / Τρέχουσα συναλλαγματική ισοτιμία] = [(1 + τρέχον ξένο επιτόκιο) / (1 + τρέχον εγχώριο επιτόκιο)]
Παράδειγμα:
Έστω ότι κάποιος επενδυτής θέλει να επενδύσει τα 100$ που διαθέτει. Έστω επίσης, ότι τα ευρωπαϊκά χρεώγραφα προσφέρουν απόδοση 5% – ενώ τα αμερικανικά 10%. Η spot (τρέχουσα) ισοτιμία EUR/USD είναι 1.09. Σύμφωνα με το θεώρημα ισοδυναμίας των επιτοκίων η μελλοντική ισοτιμία θα είναι:
Forward= Spot * (1+ieu)/(1+ius)
Όπου:
Forward= Μελλοντική Ισοτιμία
Spot= Τρέχουσα Ισοτιμία
ius = Επιτόκια ΗΠΑ
ieu = Επιτόκια Ευρωζώνης
Άρα η μελλοντική ισοτιμία θα αναμένεται να είναι:
F(e/$)= 1.09 * (1.1/1.05)
F= 1.14
Δηλαδή το ευρώ αναμένεται να ανατιμηθεί κατά 5%, το ίδιο με τη διαφορά των επιτοκίων μεταξύ των 2 χωρών.
Έτσι αν ο επενδυτής μετέτρεπε τα δολάριά του σε ευρώ (με την spot ισοτιμία) και τα επένδυε με επιτόκιο 0.05 στο τέλος του έτους θα είχε:
91.74+91.74*0.05=96.4ευρώ.
Αν κρατούσε τα 100 δολάρια και τα επένδυε με επιτόκιο 0.1 στο τέλος της περιόδου (έτος) θα είχε:
100+100*0.1=110δολάρια.
Μετατρέποντάς τα σε ευρώ με την μελλοντική ισοτιμία 1.14, θα είχε: 96.4 ευρώ ξανά.
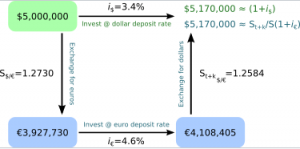
Ένα άλλο παράδειγμα με γραφική απεικόνηση:
Καλυμμένη και Μη Καλυμμένη ισοδυναμία επιτοκίων (Covered vs. Uncovered Interest Rate Parity)
Η ισοδυναμία επιτοκίων λέμε ότι είναι «καλυμμένη» όταν η συνθήκη μη ύπαρξης arbitrage μπορεί να ικανοποιηθεί μέσω της χρήσης συμβολαίων μελλοντικής εκπλήρωσης, σε μια προσπάθεια των επενδυτών να εξασφαλιστούν έναντι του μελλοντικού κινδύνου που προκύπτει από την διακύμανση των συναλλαγματικών ισοτιμιών.
Αντίστροφα, λέμε ότι η ισοδυναμία επιτοκίων είναι «μή καλυμμένη» όταν η συνθήκη μή ύπαρξης arbitrage μπορεί να ικανοποιηθεί χωρίς τη χρήση τέτοιων συμβολαίωνν.
Αρχικό άρθρο